P2P Network

Creating A Bloom Filter

In this section, we’ll use variable names that match the field names in the “filterload” message documentation. Each code block appears before the paragraph that explains it.

#!/usr/bin/env python

BYTES_MAX = 36000
FUNCS_MAX = 50

nFlags = 0

We begin by defining some maximum values from BIP37: the highest number of bytes allowed in a filter and the upper limit of hash functions that can be applied to each piece of data. We also set nFlags to zero, meaning the remote node won’t automatically update the filter for us. (While we don’t use nFlags again in this example, real applications will likely need it.)

n = 1
p = 0.0001

Here, we specify the number (n) of elements we plan to insert into the filter and the desired false positive rate (p) to help maintain privacy. In this demonstration, n is set to one element, and p is set to 1-in-10,000 to create a small, precise filter for illustration purposes. In real applications, filters would typically be much larger.

from math import log
nFilterBytes = int(min((-1 / log(2)**2 * n * log(p)) / 8, BYTES_MAX))
nHashFuncs = int(min(nFilterBytes * 8 / n * log(2), FUNCS_MAX))

from bitarray import bitarray  # from pypi.python.org/pypi/bitarray
vData = nFilterBytes * 8 * bitarray('0', endian="little")

Using the formula outlined in BIP37, we calculate the optimal size for the filter (in bytes) and the ideal number of hash functions. These values are truncated to whole numbers and constrained to the previously defined maximums. For this example, we end up with a filter of 2 bytes and 11 hash functions. Then, we use nFilterBytes to generate a little-endian bit array of the appropriate size.

nTweak = 0

We also set a value for nTweak. In this case, we simply use zero.

import pyhash  # from https://github.com/flier/pyfasthash
murmur3 = pyhash.murmur3_32()

def bloom_hash(nHashNum, data):
    seed = (nHashNum * 0xfba4c795 + nTweak) & 0xffffffff
    return( murmur3(data, seed=seed) % (nFilterBytes * 8) )

We configure our hash function template using the constant and formula from BIP37, ensuring the seed is limited to four bytes. The hash result is then taken modulo the total number of bits in the filter.

data_to_hash = "019f5b01d4195ecbc9398fbf3c3b1fa9" \
               + "bb3183301d7a1fb3bd174fcfa40a2b65"
data_to_hash = bytes.fromhex(data_to_hash)

For the data to add to the filter, we are using a transaction ID (TXID). Note that this TXID is presented in internal byte order.

print "                             Filter (As Bits)"
print "nHashNum   nIndex   Filter   0123456789abcdef"
print "~~~~~~~~   ~~~~~~   ~~~~~~   ~~~~~~~~~~~~~~~~"
for nHashNum in range(nHashFuncs):
    nIndex = bloom_hash(nHashNum, data_to_hash)

    ## Set the bit at nIndex to 1
    vData[nIndex] = True

    ## Debug: print current state
    print '      {0:2}      {1:2}     {2}   {3}'.format(
        nHashNum,
        hex(int(nIndex)),
        vData.tobytes().hex(),
        vData.to01()
    )

print
print "Bloom filter:", vData.tobytes().hex()

We apply the hash function template multiple times (once for each nHashFunc). The result of each run is used as an index, and the corresponding bit in the filter is set to 1. The debugging output helps visualize the filter’s state:


Filter (As Bits)
nHashNum nIndex Filter 0123456789abcdef
~~~~~~~~ ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~
0 0x7 8000 0000000100000000
1 0x9 8002 0000000101000000
2 0xa 8006 0000000101100000
3 0x2 8406 0010000101100000
4 0xb 840e 0010000101110000
5 0x5 a40e 0010010101110000
6 0x0 a50e 1010010101110000
7 0x8 a50f 1010010111110000
8 0x5 a50f 1010010111110000
9 0x8 a50f 1010010111110000
10 0x4 b50f 1010110111110000

Notice that during iterations 8 and 9, the filter remains unchanged because those bits had already been set earlier in iterations 5 and 7. This is expected behavior in a bloom filter.

In this example, we’ve added just one element to the filter, but this process can be repeated to add more elements. Keep in mind that a larger filter size would be required to maintain the same false positive rate as more elements are added.

For a more optimized implementation with fewer dependencies, refer to the python-bitcoinevolib bloom filter module, which is based directly on BitcoinEvo Core’s C++ implementation.

Using the “filterload” message format, the final filter created here would have the following binary form:

02 ......... Filter bytes: 2
b50f ....... Filter: 1010110111110000
0b000000 ... nHashFuncs: 11
00000000 ... nTweak: 0 (none)
00 ......... nFlags: BLOOM_UPDATE_NONE

Evaluating A Bloom Filter

The process of using a bloom filter to check for matching data is almost the same as constructing one. The main difference is that, at each step, we check if the bit at the calculated index is already set in the existing filter.

vData = bitarray(endian='little')
vData.frombytes(bytes.fromhex("b50f"))
nHashFuncs = 11
nTweak = 0
nFlags = 0

Using the bloom filter created previously, we import its key parameters. As mentioned earlier, we won’t be using nFlags to update the filter in this example.

def contains(nHashFuncs, data_to_hash):
    for nHashNum in range(nHashFuncs):
        ## bloom_hash as defined earlier
        nIndex = bloom_hash(nHashNum, data_to_hash)

        if vData[nIndex] != True:
            print("MATCH FAILURE: Index {0} not set in {1}".format(
                hex(int(nIndex)),
                vData.to01()
            ))
            return False

We define a function to check whether an element is in the provided bloom filter. When checking for a match, we determine whether the bit at a specific index in the filter is already set to 1. If the bit isn’t set, the match fails.

## Test 1: Same TXID as previously added to filter
data_to_hash = "019f5b01d4195ecbc9398fbf3c3b1fa9" \
               + "bb3183301d7a1fb3bd174fcfa40a2b65"
data_to_hash = data_to_hash.decode("hex")
contains(nHashFuncs, data_to_hash)

When testing the filter against the element we previously added, there is no output, indicating a potential match. Bloom filters are designed with a zero false negative rate, meaning they will always match items that were inserted.

## Test 2: Arbitrary string
data_to_hash = "1/10,000 chance this ASCII string will match"
contains(nHashFuncs, data_to_hash)

When testing the filter against an arbitrary string, we get the following failure output. The filter was created with a 1-in-10,000 false positive rate, which was slightly rounded up during computation, so it’s possible that an arbitrary string could have matched. However, it’s not possible to set a bloom filter with a false positive rate of zero, so your program must account for false positives. In the example output below, one of the hash functions returned an index value of 0x06, but that bit wasn’t set in the filter, causing the match failure:

MATCH FAILURE: Index 0x6 not set in 1010110111110000

Retrieving A MerkleBlock

In this section, we demonstrate how to retrieve an actual merkle block from the network and manually process it. This example walks through each step, covering basic network communication and handling of merkle blocks.

#!/usr/bin/env python

from time import sleep
from hashlib import sha256
import struct
import sys

network_string = bytes.fromhex("efb4aacf")  # Mainnet

def send(msg, payload):
    ## Command is ASCII text, padded with null characters to 12 bytes
    command = msg + ("\00" * (12 - len(msg)))

    ## Payload is converted from hex to raw bytes
    payload_raw = bytes.fromhex(payload)
    payload_len = struct.pack("I", len(payload_raw))

    ## Checksum is the first 4 bytes of SHA256(SHA256(payload))
    checksum = sha256(sha256(payload_raw).digest()).digest()[:4]

    sys.stdout.write(
        network_string
        + command
        + payload_len
        + checksum
        + payload_raw
    )
    sys.stdout.flush()

This simple Python function connects to the P2P network by computing message headers and sending payloads decoded from hexadecimal.

## Create a version message
send("version",
      "71110100" # ........................ Protocol Version: 70001
    + "0000000000000000" # ................ Services: Headers Only (SPV)
    + "c6925e5400000000" # ................ Time: 1415484102
    + "00000000000000000000000000000000"
    + "0000ffff7f000001208d" # ............ Receiver IP Address/Port
    + "00000000000000000000000000000000"
    + "0000ffff7f000001208d" # ............ Sender IP Address/Port
    + "0000000000000000" # ................ Nonce (not used here)
    + "1b" # .............................. Bytes in version string
    + "2f426974636f696e2e6f726720457861"
    + "6d706c653a302e392e332f" # .......... Version string
    + "93050500" # ........................ Starting block height: 329107
    + "00" # .............................. Relay transactions: false
)

Before a peer will accept any requests, you need to send a “version” message. Once received, the node will respond with its own “version” message followed by a “verack” message.

sleep(1)
send("verack", "")

In this basic script, we aren’t validating the peer’s “version” message, but after a short pause, we send our own “verack” message to acknowledge that we received their “version”.

send("filterload",
      "02"  # ........ Filter bytes: 2
    + "b50f" # ....... Filter: 1010 1101 1111 0000
    + "0b000000" # ... nHashFuncs: 11
    + "00000000" # ... nTweak: 0/none
    + "00" # ......... nFlags: BLOOM_UPDATE_NONE
)

Next, we load a bloom filter using the “filterload” message. This bloom filter was described in detail in the previous sections.

send("getdata",
      "01" # ................................. Number of inventories: 1
    + "03000000" # ........................... Inventory type: filtered block
    + "a4deb66c0d726b0aefb03ed51be407fb"
    + "ad7331c6e8f9eef231b7000000000000" # ... Block header hash
)

Finally, we request a merkle block that matches our bloom filter by using the “getdata” message, completing the script.

To execute the script, you can pipe it to the Unix netcat command (or one of its clones, which are available on nearly all platforms). For instance, using the original netcat and the hexdump (hd) command to display the response:

## Connect to the BitcoinEvo Core peer on localhost
python get-merkle.py | nc localhost 7333 | hd

Part of the response will be displayed in the next section.

Parsing A MerkleBlock

In the previous section, we retrieved a merkle block from the network. Now, we will walk through how to parse it. For clarity, most of the block header has been omitted here. For a more detailed hexdump, refer to the example in the “merkleblock" message section. 7f16c5962e8bd963659c793ce370d95f
093bc7e367117b3c30c1f8fdd0d97287 ... Merkle root

07000000 ........................... Transaction count: 7
04 ................................. Hash count: 4

3612262624047ee87660be1a707519a4
43b1c1ce3d248cbfc6c15870f6c5daa2 ... Hash #1
019f5b01d4195ecbc9398fbf3c3b1fa9
bb3183301d7a1fb3bd174fcfa40a2b65 ... Hash #2
41ed70551dd7e841883ab8f0b16bf041
76b7d1480e4f0af9f3d4c3595768d068 ... Hash #3
20d2a7bc994987302e5b1ac80fc425fe
25f8b63169ea78e68fbaaefa59379bbf ... Hash #4

01 ................................. Flag bytes: 1
1d ................................. Flags: 1 0 1 1 1 0 0 0

We will now parse the “merkleblock” message using the steps outlined below. Each part of the message is illustrated and explained in the corresponding paragraph.




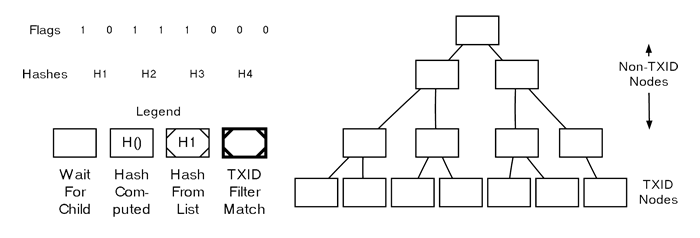
Parsing A MerkleBlock

We begin by constructing the structure of a Merkle tree, using the total number of transactions in the block as a basis.




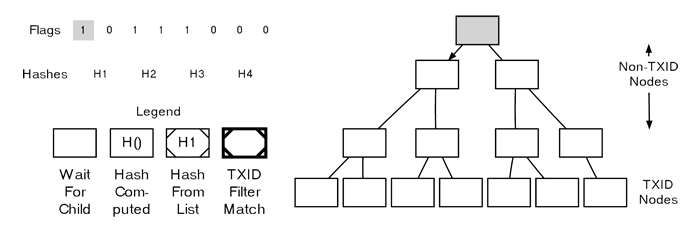
Parsing A MerkleBlock The initial flag is set to 1, and the Merkle root, as usual, represents a non-TXID node, meaning we’ll need to calculate the hash afterward using this node’s child nodes. Therefore, we move down to the left child of the Merkle root and refer to the next flag for guidance.




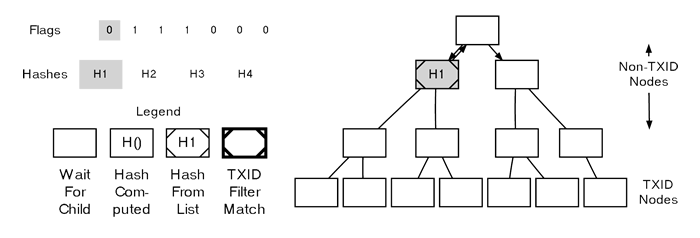
Parsing A MerkleBlock The following flag in this instance is a 0, and it also corresponds to a non-TXID node, so we apply the first hash from the “merkleblock” message to this node. We don’t need to process any child nodes either — based on the peer that generated the “merkleblock” message, none of these nodes will point to TXIDs of transactions that meet our filter, so they’re unnecessary. We then return to the Merkle root, descend into its right child, and check the next (third) flag for further instructions.




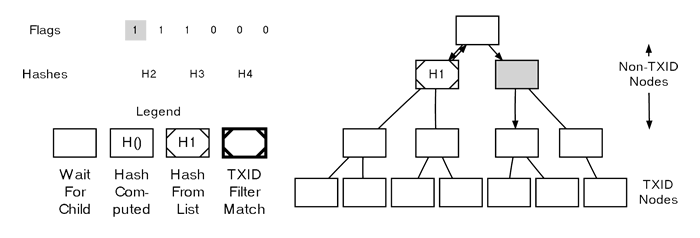
Parsing A MerkleBlock

In this example, the third flag is another 1 on a non-TXID node, prompting us to move down into its left child.




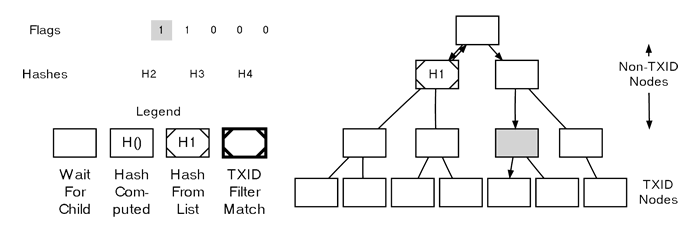
Parsing A MerkleBlock

The fourth flag is again a 1 on yet another non-TXID node, so we continue descending. We will always keep descending until we either encounter a TXID node, a non-TXID node with a 0 flag, or until the tree is completely filled.




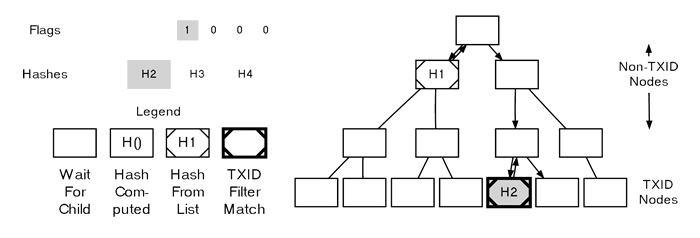
Parsing A MerkleBlock

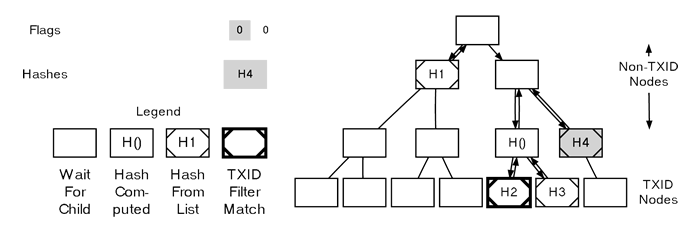
Finally, on the fifth flag in the example (a 1), we arrive at a TXID node. The 1 flag signifies that this transaction matches our filter, and we should take the next (second) hash to use as this node’s TXID.




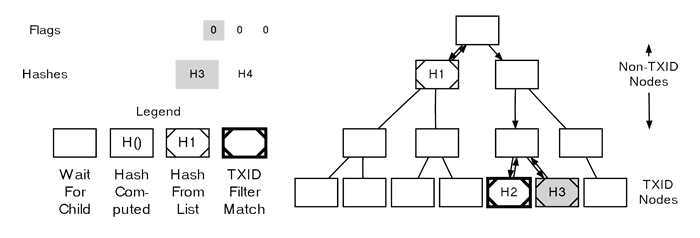
Parsing A MerkleBlock

he sixth flag also corresponds to a TXID, but it’s a 0 flag, meaning this transaction doesn’t match our filter. Nevertheless, we still take the next (third) hash and assign it as this node’s TXID.




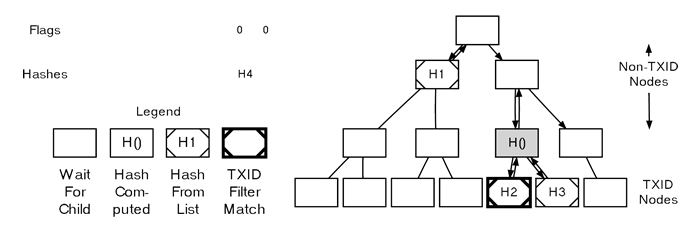
Parsing A MerkleBlock

At this point, we have sufficient information to calculate the hash for the fourth node we encountered — it’s the result of hashing the concatenated hashes of the two TXIDs we previously assigned.




Parsing A MerkleBlock

Next, we move to the right child of the third node we encountered and fill it using the seventh flag and the final hash, finding that there are no further child nodes to process.




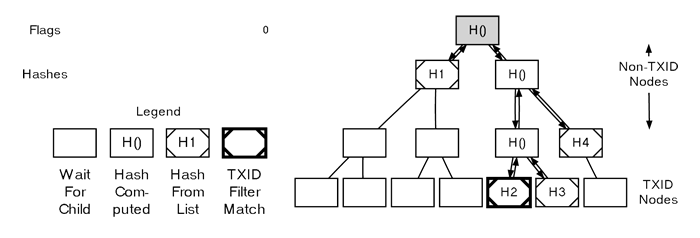
Parsing A MerkleBlock


We perform the necessary hashing to complete the tree. It’s worth noting that the eighth flag isn’t used, which is fine since it was needed to pad out a flag byte.

The last steps involve confirming that the computed Merkle root matches the one in the header and reviewing the other steps in the parsing checklist from the “merkleblock” message section.